On the Supposed Randomness of Prime Numbers

When you hear that prime numbers are randomly situated through the universe of numbers, you might reasonably assume that they can be found more or less anywhere in that universe. But that’s not entirely true. There are actually places where they can and cannot be. They may not be in some, or even most, of the places where they’re allowed to be, but they’re never in places they’re not allowed to be. They’re always in their lanes. They follow the rules.

First, rather obviously, all prime numbers larger than 2 are odd. In the table below all the numbers are lined up in 2 rows of odd and even numbers respectively. The odd numbers are shaded, and it is clear that all prime numbers larger than 2 will fall within the shaded row. I’m not saying that all the numbers in the shaded row are primes but that all primes fall within the shaded row.

We can extend this now to ask what happens to all prime numbers larger than 3. Can we construct a similar table in which all prime numbers larger than 3 fall within the same row?

And here’s how we do that:

We now have 6 rows rather than 2, and 2 shaded ones rather than 1. But we can easily see that all the prime numbers fall within them. What is a little more difficult to see is that we have not only horizontal symmetry here (i.e. if a cell is shaded, all the cells to its left and right are also shaded) but also vertical symmetry, meaning you could fold the table top to bottom and the 2 shaded rows would cover each other. This is easier to see here:

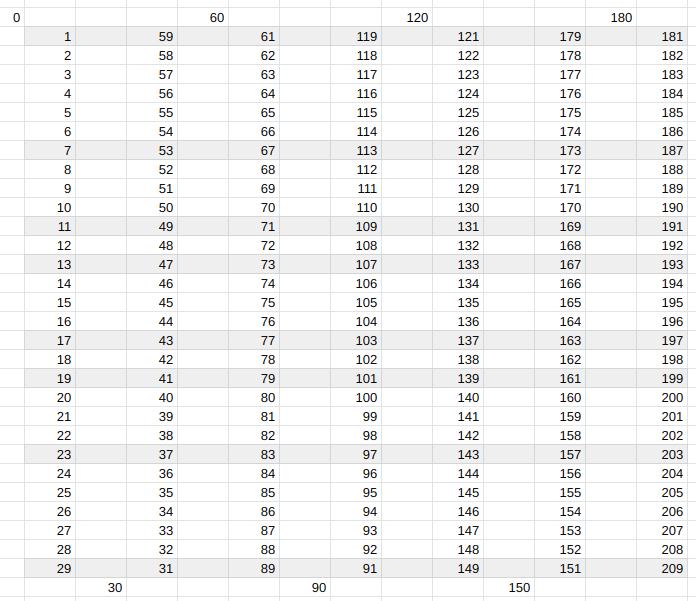
Here the numbers appear to flow more like a wave with the multiples of 6 appearing a peaks and troughs, but you will see that the symmetry remains. We can repeat this for all primes larger than 5. In the first table you will see the numbers from 0 - 30 , from 30 - 60, from 60 - 90 etc in a linear progression. In the second table you will see the wave pattern again as you read the first column top to bottom, the second from bottom to top, and so on.

Here, you will see that we have 30 rows rather than 6, and 8 shaded rows rather than 2, but the same principles apply. All prime numbers larger than 5 fall within one of the 8 shaded lines, whether you stack the numbers up in a traditional chart (the first table) or rearrange them as a wave (the second). We can fold this table top to bottom, with the “crease” through the row beginning with 15 (half of 30) and the shaded rows will cover each other exactly. This means that if you know where the primes fall in the first half of the range of numbers (e.g. from 1-15) you automatically know where they fall in the second half (e.g. from 16-30). You may not be able to predict exactly where individual primes are but you can tell, by knowing the first half of a sequence, exactly where they are allowed to be in the second half.

It’s also worth noting that these shaded lines, or prime swim lanes as I like to think of them as, clearly show where twin primes can be found across the entire universe of numbers or the numerosphere.

This applies endlessly. I would show you the charts for primes larger than 7, 11 and 13 but they have 210, 2310 and 30030 rows respectively so don’t easily fit in a blog post. And anyway, they’re very easy to make with no functions or formula other than plain addition. But you will need to know how many rows each chart will take and how many of them are shaded. This table lays out the first few:

Quite simply, the total number of rows in a chart is equal to the prime factorial for the prime being used. So, for our first chart, which was the chart of 2s, the prime factorial of 2 is 2 For the chart of 3s, the prime factorial is 2*3 = 6, for 5s, 2*3*5 = 30, for 7s, 2*3*5*7 = 210 and so on.

The number of shaded rows in a chart is equal to the prime factorials minus one for each prime. So for 2 the number of shaded rows = 2-1 = 1. For 3, the number is (2-1)*(3-1) = 2. For 5, the number is (2-1*(3-1)*(5-1) = 8, for 7, (2-1)*(3-1)*(5-1)*(7-1) = 48 and so on. The number of shaded rows equals the maximum number of primes that can be found within the total range of the factorial.

What this means is that there is symmetry in the universe of numbers, a continuous waving or looping at multiple levels, not just an endless sequential and linear, flat flow. Prime numbers are found at specific points in the those loops or waves. We may not be able to say whether a number is prime just by looking at it but we do know their swim lanes. It may not be much, but when it comes to prime numbers it’s not nothing!